• Programming
  • Tcl
    • Data file formats for Tcl scripts
    • Objects in Tcl
  • Scripting
    • Turn your scripting language into a code generator
  • Parsing
    • Parsing: introduction
    • How to avoid parsing
    • The input stream
    • Scan if you can
    • How to parse by hand
    • From recursion to grammars
    • Up and down the parsing spectrum
    • Schemas and syntax trees

Up and down the parsing spectrum

Left versus right, top versus bottom

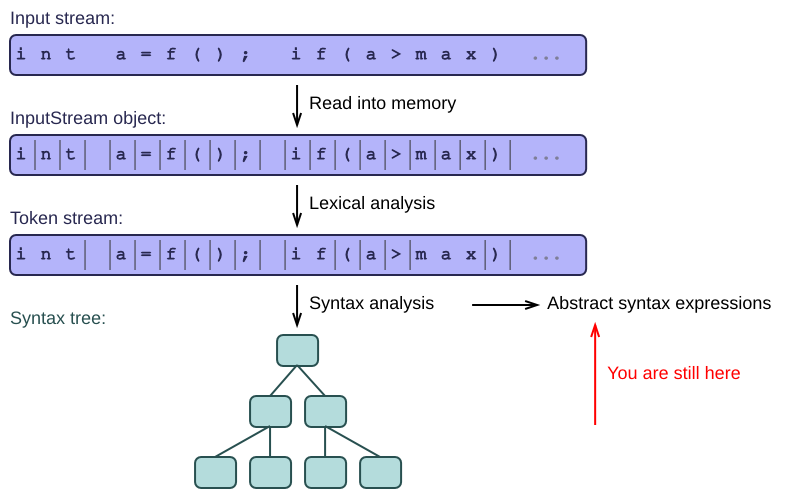
As in the previous article, we are still parsing lists of integers. Have a look at the following grammar (a major simplification relative to the ones we saw earlier):

 1 list -> int
 2 list -> list ',' int

This grammar is left-recursive, because the second syntax rule begins by invoking itself. Now, please assume for a moment that we can avoid an infinite loop here. The resulting syntax tree, not surprisingly, is left-associative, which means that the leftmost elements are grouped most tightly, and the rightmost elements are tacked at the end:

 1 3, 4, 5
 2 
 3 - list 3, 4, 5
 4   - list 3, 4
 5     - list 3
 6       - int 3
 7     - ','
 8     - int 4
 9   - ','
10   - int 5

If this is not the kind of tree you want, you have to change the grammar to make it right-recursive instead. Such a grammar has its recursive calls only at the end (i.e. at the right) of its rules:

 1 list -> int
 2 list -> int ',' list

And of course, it produces a very different parse tree, where the rightmost elements are now grouped together most tightly:

 1 3,4,5
 2 
 3 - list 3,4,5
 4   - int 3
 5   - ','
 6   - list 4,5
 7     - int 4
 8     - ','
 9     - list 5
10       - int 5

So depending on the kind of input language you're parsing, and the kind of output structure you wish to obtain, you need to adapt your grammar accordingly.

OK, now about those infinite loops. As an experienced programmer, you are aware that it is unwise to implement a function that begins by calling itself recursively. This creates an infinite loop, because the function executes its body in the order you specified. So a left-recursive function is nonsense.

But we are talking about left-recursive rules here. These syntax rules are not necessarily executed in a predefined order, remember? They are declarative, so the parsing framework is free to choose a suitable order of execution. Bottom-up parsers can handle left-recursive rules without even blinking their digital eyes. They create the parse tree from the bottom up, by grouping low-level tokens into ever bigger structures, until the syntax tree finally emerges. While grouping the tokens, they can keep many parse rules active in parallel, so they are not bothered by the left-recursion.

Top-down parsers are more familiar: they start at the top of the tree, and work their way down recursively. Our hand-written parsers are top-down; we called them "recursive descent" for this very reason. They start with the outermost functions, and then call lower-level functions until they end up invoking the lex functions at the bottom. Because of the ordering of the recursive calls, top-down parsers cannot handle left-recursion [1].

[1] Well, that's not entirely true. The OMeta framework makes clever use of a kind of caching (they call it "memoization") in which the input is cached while parsing, so that you do not have to re-parse it after backtracking. This caching mechanism clearly speeds up the parsing process. But it also allows the parser to handle left-recursion, even though it is a top-down parser. Please don't ask me how it works; it just does. See the OMeta website for more details.

If you're stuck with a more traditional top-down parser, you just have to avoid left-recursion. You can use a right-recursive grammar, but this produces different trees, which may not be what you want. Instead, you can also left-factor your grammar to remove the left-recursion! This comes at a price though: It makes the grammar more complicated, because it introduces new rules:

 1 list -> int list_tail
 2 list_tail -> ',' int list_tail
 3 list_tail -> empty

The infinite loop is gone. The resulting tree will be left-associative, but it will contain a few extra nodes of the new list_tail class. This is a rather artificial class that we had to introduce only to avoid the left-recursion.

Context-free grammars

Grammars can take many shapes and sizes, but not all of those are useful. In practice, most frameworks limit themselves to context-free grammars (or smaller subsets of those). This basically just means that the left-hand side of any syntax rule must be a single name, specifying the construct to be parsed (such as 'list'). The right-hand side then specifies one particular way of parsing that construct. Take all the rules with the same left-hand name together, and you have the complete specification for parsing the construct with that name.

All the grammars in this series of articles are context-free. The name aptly indicates that you can parse a construct without caring about the context in which it occurs. A list is always a list, whether it occurs inside the condition of an 'if' statement or as the value of a function call argument.

And here's the funny thing: Real-life programming languages are never context-free. Think about it. Let's say that our parser encounters an identifier such as 'gobbledygook' in the input. Lexically, this is just an identifier. Grammatically, we have no idea whether it represents a type name, a variable name, a function name, a namespace name, or any other kind of name. In order to figure out what 'gobbledygook' is, we need information from around the identifier. In other words, we need context.

Download any parsing framework from the web, and it will support only context-free input languages, which hardly ever occur in practice. Does this mean that parsing frameworks are useless? Hardly. We just need to extend them, that's all.

For identifiers, we extend the frameworks with a symbol table that keeps track of all the names (also known as "symbols") in our input program. We look up the name 'gobbledygook' in the symbol table, and we obtain information about what it represents (a function, a variable, a namespace, etc). We then use that information to guide the parsing process, i.e. to select the syntax rule for a FunctionCall or VariableUse or Namespace.

Symbol lookup is not part of any grammar. It cannot be expressed in PEGs or in declarative grammars. It needs to be attached to an existing grammar, typically by means of attached actions as described in the previous article. This is how you can sneak some context-sensitive information into an otherwise context-free grammar.

How to deal with ambiguity

Here are 3 grammars for parsing integer-lists. See if you can spot the difference:

 1 // Grammar 1: left-recursive
 2 list -> int
 3 list -> list ',' int
 4 
 5 // Grammar 2: right-recursive
 6 list -> int
 7 list -> int ',' list
 8 
 9 // Grammar 3: both-recursive?
10 list -> int
11 list -> list ',' list

We already talked about the first two of these, so let's see what's behind door number 3. If you use this grammar to parse our familiar input list "3,4,5", you will notice that you can end up with both the left- and right-associative syntax tree, depending on the choices you make when recursing. You go down the leftmost occurrence of 'list' first, and you find yourself with a choice: Either parse a single int (as in the right-recursive grammar), or parse a whole new list (left-recursive). These choices lead to two different output trees. This unwanted flexibility has a name: Ambiguity.

Don't worry, we can easily remove this ambiguity. Just use either the left- or right-recursive grammar, and you're safe. But in general, can grammars always be rewritten to make them totally unambiguous? Yes and no.

You can never write a tool that discovers all ambiguities in a grammar, because this has been shown to be an undecidable problem. Just imagine writing an algorithm that takes a set of rules, and needs to find out if any input stream can lead to more than 1 output structure. I mean, you have to try all possible inputs, not just a sample. Impossible.

Luckily, there is a subset of context-free grammars for which ambiguity detection is decidable. These are the LL and LR grammars you may have heard about. Antlr is an example of a parsing framework that limits itself to such a decidable subset of grammars. It is very powerful: It throws an error if you give it an ambiguous grammar. It detects these ambiguities statically, so you can clean up your grammar before sending it off to the customer.

This article is not a tutorial on how to parse arithmetic expressions such as 1+2*3. But I have to mention this: Ambiguity is a big deal when it comes to parsing such expressions. There is a huge difference between (1+2)*3 and 1+(2*3), as I hope you can calculate. So you'd better make sure that your grammar makes the correct choices between left- and right-associativity. This is typically done by writing a huge set of syntax rules, one for each operator (or actually one for each precedence level). The resulting grammar is not ambiguous anymore, but it is much more verbose and complicated than the one you thought you could get away with. When you remove ambiguity, you often have to make your grammar more complicated. This is one of those facts of life that seems unavoidable [2].

[2] For the case of arithmetic expressions, there is a very elegant solution which I hope to show you in a later article.

PEGs do not have ambiguity (or they "ignore" it), because they use a fixed ordering of the rules. They always end up with the same tree, because they do not have to make choices between equivalent rules. They always just choose the first one, end of story. Of course, PEGs still have to deal with precedence levels and associativity when parsing an expression, but we go into that in a later article.

Top-down parsers

Hand-written parsers are naturally top-down, because your higher-level functions call lower-level ones explicitly. The same is true for PEGs, which are very close to hand-written parsers in many aspects. The OMeta framework is a typical example of a PEG parser, although it adds a few twists of its own (such as supporting left-recursion).

In the land of declarative grammars, top-down parsers are typically known as LL parsers. There is undoubtedly a very good reason for giving them such an alien name, but the main point to remember is simply that these parsers are top-down. This implies a number of things:

• LL grammars are closer to what you would write by hand.
• LL frameworks are often easier to implement and understand.
• LL grammars do not support left-recursion, because that would cause infinite loops. So you need to use techniques for eliminating left-recursion, resulting in a more complicated grammar and a larger syntax tree.

LL parsers are extremely popular, due to their simplicity and wide availability. Antlr is the most famous one. It is very robust and user-friendly, but often lacking in good documentation.

LL parsers often require semantic actions, to help disambiguate the input. Antlr allows you to attach actions to the rules, written in one of the supported programming languages (including, naturally, C). In Antlr, you can also attach predicates to the syntax rules. These are a kind of if-statements which prevent a rule from being applied if its conditions are not met. You typically use these conditions to perform semantic checks which cannot be expressed directly in the grammar. Writing actions and predicates is fairly easy, because the parsing process is intuitive (close to hand-written).

Many LL parsers require some form of look-ahead. This means that they sometimes need to read several tokens to figure out which syntax rule to invoke. Without look-ahead, the parser would try one syntax rule after another, and then backtrack when it fails. Backtracking is quite expensive, because it needs to undo a lot of the work and then redo it when trying the next rule. Look-ahead is already a bit faster, because it chooses the correct rule right away. But we can do even better than that and select the correct rule without look-ahead. Read on.

Predictive parsing (without look-ahead)

Predictive parsing is a form of top-down parsing without backtracking. Multiple rules in your grammar might have the same prefix, i.e. they begin with the same parts:

 1 statement -> if then
 2 statement -> if then else

Such rules are obviously ambiguous: Which one do we use when we encounter an 'if' in the input? We could use look-ahead to find an 'else' further in the token stream. But we could also eliminate the common prefix by introducing an extra rule:

 1 statement    -> if then statement2
 2 statement2   -> else
 3 statement2   -> empty

The parser can now just steam ahead and use the only rule that begins with 'if'. It needs to make a choice only when parsing statement2, but this choice is based on the single next token which is either 'else' or something else ;-) You can see why this technique is called "predictive parsing": The parser just knows which rule to apply; it can predict the future.

Note that this technique again makes the grammar more complex: It requires a new rule and a new artificial grammar element called 'statement2' which pollutes your syntax tree.

You can come up with even more complex examples that require a fixpoint algorithm to eliminate all prefixes and make the grammar predictive. The algorithm determines the "first-sets", which are the sets of element that are allowed at the start of a rule. Only those elements then have to be considered when selecting a rule to apply. This is way beyond the scope of our article, and in fact way beyond my own brain capacity, so forget I said anything.

Bottom-up parsers

Donald Knuth invented a completely different approach to parsing, which builds the syntax tree from the leaves up to the root. The fact that Knuth is one of the most brilliant computer scientists, as in ever, should be a warning for anyone bold enough to try to write a new bottom-up parser from scratch. Don't try this at home, kids.

In practice, bottom-up parsers are never written by hand, but generated by a framework from an LR grammar. These parsers are notoriously hard to debug and understand, so I won't even begin to try. All I know is that the parsing algorithm is based on so-called shift-reduce steps, where tokens are shifted from the input into a buffer, and then a sequence of these tokens gets replaced by (or "reduced to") the left-hand side of a grammar rule. The parser can keep many such rules under consideration in parallel, so it's decidedly declarative.

The biggest advantage of LR parsers is that they allow left-recursion. In fact, left-recursion is even preferred, because it allows for faster reductions, making the parser more Speedy Gonzalez.

LR parsers can also handle a slightly larger set of grammars than LL parsers. This is not very useful in practice, because most existing programming languages can be easily parsed in LL style anyway.

LALR is a slightly restricted set of grammars, allowing for much better performance than general LR. Yacc and Bison are typical examples of this kind of parser. They are well-known in the linux community, and well-documented all around the web.

Advanced parsers

If your head isn't spinning yet, you could study even more advanced forms of parsing. I just mention these briefly here to give you a starting point for further exploration, but please don't press me for details. I'm not ashamed to admit that most of this sutff goes way over my uncombed hair.

GLR parsers apparently succeed in running in linear time (for unambiguous grammars). They are advertised to handle all context-free grammars, and to deal with ambiguity gracefully (which must be quite a trick, since ambiguity is known to be undecidable). Now the nice thing about context-free grammars is that they are closed under composition, meaning that you can extend such a grammar with new rules and the result will always still be context-free. More restricted sets of grammars, such as LL or LR, are not closed, so they break easily when adding new rules.

Finally, left-corner parsing is a hybrid technique: it starts out as LR (bottom-up), but as soon as the syntax rule is unambiguously known, it switches to LL (top-down). This apparently combines the benefits of both.

Theory versus practice

After all this declarative parsing theory, I have to make a confession. I never actually use declarative grammars at all. I prefer PEGs.

PEGs offer all the wins (abstraction, brevity, high performance) without any of the losses (ambiguities, complexity, steep learning curve). In a declarative setting, you have to add various complications to you grammars to allow for context-sensitive information, to eliminate left-recursion, to eliminate ambiguity, etc. PEGs on the other hand, are never ambiguous, never left-recursive, and much closer to what you and I would write by hand.

PEGs still require context information (such as a symbol table), but you can easily integrate them into a schema-based approach (which we will discuss later). Inside a schema, the syntax rules have intimate knowledge of the syntax nodes and their attributes, so they can be integrated much more tightly with the symbol table and other semantic processing. Context information becomes much more natural and readily available in such a setting. The result is an integrated solution for parsing and semantically resolving input programs, and it is by far my preferred way of working.

Because I often write recursive-descent parsers by hand, or use PEGs and schema-based parsing, I never have to deal with LL and LR parsing, ambiguity and left-factoring, context-freeness and context-sensitivity, and all the other rocket science in this article.